(1)非定常信号抽出方法
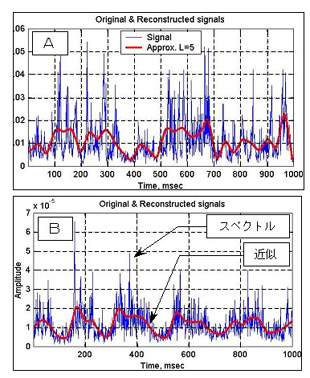
デュアルタイム周波数領域の非定常信号に対して、JTFA(Joint-Time-Frequency-Analysis)を適用した。20kHz周辺の比較的狭周波数帯が、検出最適化領域として選定された。非定常信号抽出に、この周波数帯中の狭周波数帯における信号の時間依存出力要素を、用いることとした。JTFAにおいてはガボール変換を用いて、時間周波数特性から時間依存出力値を抽出する。抽出された時間依存出力値は、ガボール係数の2乗に等しい値となる(図8.6.12参照)。
ウェーブレット解析により抽出された時間依存出力値を、信号のエンベロープに変換する。エンベロープは、信号ひずみの影響を受けにくいため、信号処理に非常に有効である。離散ウェーブレット変換(DWT)に基づくウェーブレット分析は、信号を細かな構成要素にするための有効なツールである。元の信号及びその構成要素の復元は、DWT係数により可能となり、位相ひずみも少なくなり、望ましいエンベロープを作成することができる。(図8.6.13参照)
(2)相関行列検出手法(Correlation Matrix Method)
相関行列検出手法は、エンベロープの相関行列と |
|
して提案されたものである。検出パラメータとして提案されている相関行列は、以下の式(7)により表される。
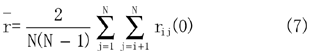
i,j:周波数バンドの添字
N:周波数バンドの総数
rij(0):規格化相関係数
背景騒音が、各周波数に対して低相関値である場合(0〜0.7の範囲、平均値0.3)、実際の非定常漏えい信号(約0.8)及び仮想バースト信号(約0.9)は、高い相関行列が得られる。
この相関特性は、サイトの各種マイクロフォン位置について解析された。また、その相関特性は、模擬漏えい音発生装置から7mまでの、距離における微小漏えいを検知する。相関行列は、-10dBまでのSNRにおける非定常漏えい信号を検出するため、使用することが可能であることが分かった(図8.6.14参照)。
|